Adatok
meko
13 bejegyzést írt és 17 hozzászólása volt az általa látogatott blogokban.
A matematikát és a logikát manapság kevésbé szerencséltetik a hóbortos világmegváltók és csodadoktorok, mint amennyire divatos dolog rákgyógyszereket, fogyasztó csodaszereket, vagy első- és másodfajú örökmozgókat előállítani, esetleg felfedezni nyelvünk és népünk sumer vagy sziriuszi gyökereit. A…..
meko
2010.10.01 13:25:04
@Amaranta: A korlátlan komprehenzió elvét senki nem tartja érvényesnek, ebbőpl ugyanis minden további feltevés nélkül következik a Russell-paradoxon.
Az állítás az, hogy a _naiv halmazelméletben_ érvényes a korlátlan komprehenzió elve. Ez ugyanis egy ellentmondásos elmélet.
Hogy Cantor pontosan hogy vélekedett a korlátlan komprehenzióról (elmélete milyen mértékben fedte azt, amit ma naiv halmazelméletnek nevezünk), az nem egyszerűen megválaszolható, de történészek által hálistennek bőségesen tárgyalt kérdés. Az általam ismert legjobb írás a témában M. Hallett "Cantorian Set Theory and Limitation of Size" című könyve (Clarendon, Oxford, 1984, google book formában online olvasható), amelyet vitánk során Geier úr figyelmébe ajánlottam. Történeti ismeretek nélkül az axiomatizálás előtti halmazelmélet témájához nem lehet érdemben hozzászólni.
Az állítás az, hogy a _naiv halmazelméletben_ érvényes a korlátlan komprehenzió elve. Ez ugyanis egy ellentmondásos elmélet.
Hogy Cantor pontosan hogy vélekedett a korlátlan komprehenzióról (elmélete milyen mértékben fedte azt, amit ma naiv halmazelméletnek nevezünk), az nem egyszerűen megválaszolható, de történészek által hálistennek bőségesen tárgyalt kérdés. Az általam ismert legjobb írás a témában M. Hallett "Cantorian Set Theory and Limitation of Size" című könyve (Clarendon, Oxford, 1984, google book formában online olvasható), amelyet vitánk során Geier úr figyelmébe ajánlottam. Történeti ismeretek nélkül az axiomatizálás előtti halmazelmélet témájához nem lehet érdemben hozzászólni.
meko
2010.10.01 14:55:09
@Amaranta: "GJ pedig azt bizonyította be matematikai levezetéssel, hogy a komprehenzió elve nem érvényes bijektív leképezés feltételezése mellett a naiv halmazelméletben."
Ezt nem értem. A naiv halmazelméletben posztuláljuk a korlátlan komprehenziót. Ennyiben tehát érvényes. Másfelől, mivel az elmélet ellentmondásos, a komprehenziós sémának megfelelő bármely konkrét formula tagadását is le tudjuk vezetni. Tehát érvényes is meg nem is. Ez egy hibás elmélet, több szót kár is rá vesztegetni.
Ettől teljesen független kérdés, hogy a Cantor-bizonyítás működik-e vagy sem. Naiv halmazelméletben működik, ZFC-ben is működik, Quine halmazelméletében viszont nem működik, mert a diagonális komprehenzió nem rétegzett.
Geier úr gondolatmenetével ott kezdődnek a bajok, hogy nem teszi világossá, a halmazelmélet melyik verziójában dolgozik, tehát hogy pontosan milyen halmazelméleti előfeltevésekkel él; hanem ehelyett valamiféle homályosan körülírt "természetes matematikai gondolkodásra" hivatkozik, amelyet történeti indoklás nélkül érvényesnek tart a matematikának a modern matematikai logika standardjeinek kialakulása előtti állapotára.
Ezt nem értem. A naiv halmazelméletben posztuláljuk a korlátlan komprehenziót. Ennyiben tehát érvényes. Másfelől, mivel az elmélet ellentmondásos, a komprehenziós sémának megfelelő bármely konkrét formula tagadását is le tudjuk vezetni. Tehát érvényes is meg nem is. Ez egy hibás elmélet, több szót kár is rá vesztegetni.
Ettől teljesen független kérdés, hogy a Cantor-bizonyítás működik-e vagy sem. Naiv halmazelméletben működik, ZFC-ben is működik, Quine halmazelméletében viszont nem működik, mert a diagonális komprehenzió nem rétegzett.
Geier úr gondolatmenetével ott kezdődnek a bajok, hogy nem teszi világossá, a halmazelmélet melyik verziójában dolgozik, tehát hogy pontosan milyen halmazelméleti előfeltevésekkel él; hanem ehelyett valamiféle homályosan körülírt "természetes matematikai gondolkodásra" hivatkozik, amelyet történeti indoklás nélkül érvényesnek tart a matematikának a modern matematikai logika standardjeinek kialakulása előtti állapotára.
Még most, a poszt elején felhívom a kedves olvasó figyelmét, hogy szigorúan az én saját szubjektív magánvéleményem az, amiről most írni fogok. Többször is terveztem már, de most jutottam el oda, hogy meg is teszem. Sosem rejtettem véka alá, hogy vagyok olyan lusta és kényelmes,…..
meko
2010.09.21 22:28:04
Első, de talán második ránézésre is megállapíthatjuk, hogy az alma nem esett messze a fájától. Sőt, olyannyira közel landolt, hogy követve a fontos anya-képet rögtön maga alá kapott pár kereket, így róhatja ő is az utakat. A képet szemügyre véve érezhetjük a generációk…..
meko
2009.04.10 13:24:37
@dJw_: Miért? Mi nem jó vagy nem valószerű benne?
Budapesten most már visszavonhatatlanul beköszöntött a tavasz. Kerékpárosok özönlötték el az utakat. Az utóbbi időben jobbára nők szerepeltek az oldalon; most néhány kerékpáros férfit mutatunk be. Fotó: Polgárdi Ákos..
meko
2009.04.10 13:14:42
@Csáki István: Miért is lenne? :-)
www.yehudamoon.com/index.php?date=2009-03-31
(Aki a sisak szükségességéről szeretne eszmét cserélni, annak javaslom a http:criticalmass.hu fórumot.)
www.yehudamoon.com/index.php?date=2009-03-31
(Aki a sisak szükségességéről szeretne eszmét cserélni, annak javaslom a http:criticalmass.hu fórumot.)
A kép még Bringaexpón készült, készítője: Éder Veronika Te mibe pakolsz?..
meko
2009.04.07 15:46:37
Piros pont annak, aki megmondja, milyen rendezvény plakátján szerepel a hölgy! Fotó: Timár Gergely..
Hányszor halljuk, hogy „jaj, muszáj autóval mennem, gyerekkel vagyok”! Vajon hol jobb a babának? A hátsó ülésen, vagy anya, apa hátán?Fotó: Prof..
meko
2009.03.28 23:31:58
Nem kell ahhoz nagy flanc, hogy valaki csinos legyen a biciklin.
Fotó: JP..
Van egy jó fényképed a bringádról? Küldd be! Nincs? Ne habozz, fényképezz! Idézet a kiírók leveléből: Nekünk roppant izgalmas lehetőség lenne a Cycle Chic olvasóitól fotókat kapni kedvenc verdájukról… legyen szó bármilyen pedálos szerkezetről is. Ha esetleg valami…..
Fotó: pohly@..
meko
2009.03.26 13:45:01
@dJw_: Cserébe öltönyös, és nyélen rakja. Ez egyelőre elég ritka, és kimondottan viágvárosi jelenség. Azért tettük be a fotót életlenül is, mert fontos jelensléget mutat, és sajnos egyelőre nem olyan könnyű ilyet elcsípni, mint bringaúton mosolygó szoknyásokat.
Fotó: Hamvas Bálint, a képen reku papa..
Kőkemény csajok a flaszteren. 1. fotó: Matt. 2. fotó: Repeet...
meko
2009.03.23 01:46:20
@lmariann: Ez egyre rejtélyesebb! :-) Áronnal a dátumok ismerete nélkül arra jutottunk, hogy ugyanaz a kislány szerepel a képeken; ezek szerint mégsem?
meko
2009.03.23 18:08:25
@nyehljudov: Na, lassan csak kiderülnek a dolgok! :-) Stram lányod van, gratulálok! A bekezdés szövegét meg megint átírom.
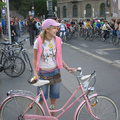
A bringa neve: Selyemcukor. Fotó: Hargita Nándor..
meko
2009.03.22 10:25:03
A mosolygós anyukának a kormány mögé van szerelve egy gyerekülés, hogy a baba se maradjon ki az utca látványából, és a mama közelségéből...
meko
2009.03.20 01:31:50
...mindig mosolyogva, mindig magassarkúban!Fotó: Tarcali Dávid..
Belépve többet láthatsz. Itt beléphetsz
- Peter Aczel halmazelmélete:
en.wikipedia.org/wiki/Non-well-founded_set_theory
- Quine halmazelmélete:
en.wikipedia.org/wiki/New_foundations
- R. Holmes kiváló áttekintése a témáról:
plato.stanford.edu/entries/settheory-alternative/