Adatok
malvázia
0 bejegyzést írt és 20 hozzászólása volt az általa látogatott blogokban.
Örülünk, Vincent?
Matolcsy György esete a magyar felsőoktatással és az orbáni elittel
2020.06.29 14:51:18

Matolcsy György ma egy tizenkét pontból álló jövőképet vázolt fel a növekedés.hu oldalon.
******************************************************************************************
" A történelmi tanulságok alapján 2030-ra szükségünk van:
Teljes demográfiai fordulatra,…..
malvázia
2020.06.29 19:08:48
@jotunder: a helyes leíráshoz némi koncentráltság szükségeltetik, de kimondani az pofonegyszerű: "Vagadogu"

– A matematikát tartjuk a legegzaktabb tudománynak. Rengeteg törvényszerűsége van, ám az 1930-as években egy osztrák matematikus, Kurt Gödel kitalált egy olyan formulát, amely csak akkor igaz, ha nem bizonyítható. A részletekbe nem megyek bele, a lényeg az, hogy még a matematika sem…..
malvázia
2019.01.10 05:10:22
@Bourbaki:
> A Pitagorasz-tétel átdarabolós bizonyítása is axiomatikussá válik, ha kirészletezzük, hogy pontosan miért is működik.
Azért hoztam fel ezt a példát, mert ez egy ritka péla arra, hogy mást csinálunk az intuitív matekban, mint a formálisban.
Legtöbbször a naivnak elkönyvelt gondolatmenetek intaktak maradnak attól, hogy az alattuk levő fogalmi apparátust formalizáljuk. Azt, hogy hogy látod be, hogy végtelen sok prímszám van, nem fog váltzoni attól, hogy naiv matekről formálisra váltasz (a gondolatment érvényességének értelmezése változik ekkor, de maga a gondoltatmenet marad).
A Pitagorasz-télelt rohadtul nem átdarabolással látod be a formalizálás után, hanem ez egy trivialitás, mert a síkbeli távolságfogalmat épp úgy definiáltuk, hogy igaz legyen. Szóval 1) volt a naiv átdarabolós bizonyítás 2) volt a sík, mint ℝxℝ formalizáció 3) a Pitagorasz-tételből eredő motivációból be lett vezetve a gyök ( áegyminuszbéegynégyzet plusz ákettőnégyzetmínuszbékettőnégyzet) definíció. Szóval lényegében a naiv tétel formális definícióvá vált.
> A Pitagorasz-tétel átdarabolós bizonyítása is axiomatikussá válik, ha kirészletezzük, hogy pontosan miért is működik.
Azért hoztam fel ezt a példát, mert ez egy ritka péla arra, hogy mást csinálunk az intuitív matekban, mint a formálisban.
Legtöbbször a naivnak elkönyvelt gondolatmenetek intaktak maradnak attól, hogy az alattuk levő fogalmi apparátust formalizáljuk. Azt, hogy hogy látod be, hogy végtelen sok prímszám van, nem fog váltzoni attól, hogy naiv matekről formálisra váltasz (a gondolatment érvényességének értelmezése változik ekkor, de maga a gondoltatmenet marad).
A Pitagorasz-télelt rohadtul nem átdarabolással látod be a formalizálás után, hanem ez egy trivialitás, mert a síkbeli távolságfogalmat épp úgy definiáltuk, hogy igaz legyen. Szóval 1) volt a naiv átdarabolós bizonyítás 2) volt a sík, mint ℝxℝ formalizáció 3) a Pitagorasz-tételből eredő motivációból be lett vezetve a gyök ( áegyminuszbéegynégyzet plusz ákettőnégyzetmínuszbékettőnégyzet) definíció. Szóval lényegében a naiv tétel formális definícióvá vált.
malvázia
2019.01.10 06:36:18
@Bourbaki:
> nem látok a számok és a halmazok között nagy ontológiai különbséget
Fussunk ennek neki mégegyszer.
Vegyük ezt a furi fogalmat, hogy "független állítás". Van olyan, hogy halmazemélettől (ZFC-től, vagy bármelyik másik épkézlábtól) független állítás. Meg persze olyan is van, hogy PA-tól, meg egyéb axiómarendszerektől független állítás. De olyanról nem beszélünk, hogy az aritmetikától (nem a Peano, hanem a valódi aritmetikától) független állítás! Mert az aritmetika az konkrét, és minden aritmetikai állítást kiértékel igazra vagy hamisra. Az aritmetika az intuíciónkon keresztül konkrét, nem egy axiómarendszer által. A halmazelmélet viszont definíció szerint a ZFC, egy axiómarendszer.
Igazából még a legelszántabb formalista is platonista kell hogy legyen legalább a természetes számokat illetőleg. Ugyanis szerinte a matematika valójában a ZFC-ből végzett formális levezetések világa. De hogy ez értelmezhető legyen, ahhoz a naiv szinten érteni kell, hogy mi az a levezetés és levezethetőség (azaz a levezetések univerzumát kell ésszel felfognunk, mivel az ebben való előfordulás a levezethetőség). Ez meg ugyanaz a kognitív szint, mint a természetes számoké, tehát az, hogy vannak ilyen bigyók, amiket egymás után raksz, és akármennyit egymás után rakhatsz belőlük.
Tehát tudjuk, mik azok a természetes számok, különben nem tudnánk a formalizmushoz szükséges metamatematikai apparátus sem állna rendelkezésünkre.
Ha a halmazok ugyanezen az ontológiai szinten lennének, akkor tudnánk mik a halmazok. De nem tudjuk, mert amennyit tudunk róluk, az annyira vague, hogy független állításoknak ad teret.
Szóval ne kerülgessük a forró kását, mondd meg, mik azok a halmazok!
- A formalista erre azt mondja, na ne viccelj, bilibe lóg a kezed, talán már tudod, hogy Mikulás igazából nem létezik, s olyanok, hogy halmazok sincsenek igazából, van ZFC meg az onnan kiinduló levezetések.
Ez elég más ontológia -- konkrétan nihilista ontológa --, mint amit a természetes számoknál kifejtettünk az előbb.
- A platonista tendenciákkal bírók meg azt mondják, hogy hát igen, olyan konkrétan ezt nem tudom megmondani, itt kérem multiverzum van, azok bármelyikében lakozhatok, s igazából nem is érdekel, melyikben lakozom, csak legyenek biztosítottak a lakhatási feltételek.
Oké, szóval csak az érdekel, hogy teljesüljön a ZFC, nade *miben*? Ha nem csak formulabaszogatás a halmazelmélet, hanem teljesülnie is kéne valahol, akkor mi a lehetséges univerzumok köre? Ha axiómákból indulsz ki és nem vagy ontológialag nihilista, akkor kell valami kvázi modellelméletet fabrikálnod, hogy legyen hol kiértékelned a formuláidat. Ha már van halmazelméletünk, abban könnyű modellelméletet csinálni, a modell-jelölt egy tetszőeges halmaz a megfelelő relációs és algebrai szignatúrával felszerelve. De most még nincs!
Tehát már a halmazelmélet modellelméleti kerete is bizonytalan -- hogy ne lenne ez akkor más ontológialag, mint a természetes számok konkrétsága?
> nem látok a számok és a halmazok között nagy ontológiai különbséget
Fussunk ennek neki mégegyszer.
Vegyük ezt a furi fogalmat, hogy "független állítás". Van olyan, hogy halmazemélettől (ZFC-től, vagy bármelyik másik épkézlábtól) független állítás. Meg persze olyan is van, hogy PA-tól, meg egyéb axiómarendszerektől független állítás. De olyanról nem beszélünk, hogy az aritmetikától (nem a Peano, hanem a valódi aritmetikától) független állítás! Mert az aritmetika az konkrét, és minden aritmetikai állítást kiértékel igazra vagy hamisra. Az aritmetika az intuíciónkon keresztül konkrét, nem egy axiómarendszer által. A halmazelmélet viszont definíció szerint a ZFC, egy axiómarendszer.
Igazából még a legelszántabb formalista is platonista kell hogy legyen legalább a természetes számokat illetőleg. Ugyanis szerinte a matematika valójában a ZFC-ből végzett formális levezetések világa. De hogy ez értelmezhető legyen, ahhoz a naiv szinten érteni kell, hogy mi az a levezetés és levezethetőség (azaz a levezetések univerzumát kell ésszel felfognunk, mivel az ebben való előfordulás a levezethetőség). Ez meg ugyanaz a kognitív szint, mint a természetes számoké, tehát az, hogy vannak ilyen bigyók, amiket egymás után raksz, és akármennyit egymás után rakhatsz belőlük.
Tehát tudjuk, mik azok a természetes számok, különben nem tudnánk a formalizmushoz szükséges metamatematikai apparátus sem állna rendelkezésünkre.
Ha a halmazok ugyanezen az ontológiai szinten lennének, akkor tudnánk mik a halmazok. De nem tudjuk, mert amennyit tudunk róluk, az annyira vague, hogy független állításoknak ad teret.
Szóval ne kerülgessük a forró kását, mondd meg, mik azok a halmazok!
- A formalista erre azt mondja, na ne viccelj, bilibe lóg a kezed, talán már tudod, hogy Mikulás igazából nem létezik, s olyanok, hogy halmazok sincsenek igazából, van ZFC meg az onnan kiinduló levezetések.
Ez elég más ontológia -- konkrétan nihilista ontológa --, mint amit a természetes számoknál kifejtettünk az előbb.
- A platonista tendenciákkal bírók meg azt mondják, hogy hát igen, olyan konkrétan ezt nem tudom megmondani, itt kérem multiverzum van, azok bármelyikében lakozhatok, s igazából nem is érdekel, melyikben lakozom, csak legyenek biztosítottak a lakhatási feltételek.
Oké, szóval csak az érdekel, hogy teljesüljön a ZFC, nade *miben*? Ha nem csak formulabaszogatás a halmazelmélet, hanem teljesülnie is kéne valahol, akkor mi a lehetséges univerzumok köre? Ha axiómákból indulsz ki és nem vagy ontológialag nihilista, akkor kell valami kvázi modellelméletet fabrikálnod, hogy legyen hol kiértékelned a formuláidat. Ha már van halmazelméletünk, abban könnyű modellelméletet csinálni, a modell-jelölt egy tetszőeges halmaz a megfelelő relációs és algebrai szignatúrával felszerelve. De most még nincs!
Tehát már a halmazelmélet modellelméleti kerete is bizonytalan -- hogy ne lenne ez akkor más ontológialag, mint a természetes számok konkrétsága?
malvázia
2019.01.11 21:42:14
@Bourbaki:
> Gödel konstruálható univerzuma:
Tudtommal ez egy halmazelméleten belüli konstruckió, és halmazok egy teljes vertikumban végighúzódzkodó alosztályát definiálja, amit traszfinit, rendszámokkal indexelt konstrukció ad ki. Ennek fényében a "mik a halmazok?" kérdéshez nemigen ad támpontot... (Mármint a konstukció transzfinit volta miatt nem látom, hogy lehetne a halmazelméleti keretből kiemelve egy naiv / meta-matematikai variánst tető alá hozni..)
> De hol húzzuk meg a határt?
Igen, szerintem ez az izgalmas kérdés, ami elsikkadt. Amúgy nem is kell rá feltétlen éles választ adni, az is jó, ha egy meta-matematikai szempontból elég combos toolkitről el tudjuk fogadni, hogy e határon belül van.
> Gödel konstruálható univerzuma:
Tudtommal ez egy halmazelméleten belüli konstruckió, és halmazok egy teljes vertikumban végighúzódzkodó alosztályát definiálja, amit traszfinit, rendszámokkal indexelt konstrukció ad ki. Ennek fényében a "mik a halmazok?" kérdéshez nemigen ad támpontot... (Mármint a konstukció transzfinit volta miatt nem látom, hogy lehetne a halmazelméleti keretből kiemelve egy naiv / meta-matematikai variánst tető alá hozni..)
> De hol húzzuk meg a határt?
Igen, szerintem ez az izgalmas kérdés, ami elsikkadt. Amúgy nem is kell rá feltétlen éles választ adni, az is jó, ha egy meta-matematikai szempontból elég combos toolkitről el tudjuk fogadni, hogy e határon belül van.

Van ez az öt pont, amit az ellenzéki képviselők decemberben be akar(n)tak olvastatni a közmédiában, mert rájuk tört a forradalmi hevület, és ha teszem azt, odabent van egy Táncsics vezetéknevű alkalmazott, foggal szabadítják ki a Kunigunda úti vágószobából, de hát nem volt.
Szóval mentek Szél…..
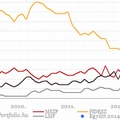
A Medián 14 százalékos támogatottságot mért a teljes népességben a felmérést megelőző napokban alakult Együtt 2014-nek (a biztos szavazó pártválasztók között meg 22 százalékot). Az eredmény nagyon meglepett. Nem azért, mert kétségbe vonnám, hogy valós választói igény…..
malvázia
2012.11.12 16:07:32
A Medián konkrét számai másodlagosak. Az eredményük csupán egy elismert + bevett módszertannal (közvéleménykutatás) való visszaigazolása annak, amit amúgy is, anélkül is, mindenki tud vagy tudnia kéne. A Medián eredményét baszogatni olyan, mint amikor ráz a hideg veszettül, megméred a lázad, 39,3-at mutat a hőmérő, és akkor azon kezdesz el lamentálni, hogy de lehet basszus, hogy nem volt jól lerázva a mérő a mérés előtt. Le van szarva, ráz a hideg vagy sem?
A centrumból réges-rég kivonult mindenki, iszonyatos űr tátong ott, és nagyon erős keresleti igény van a 8 év ballib, majd 2 év fidesznyik kormányzásból rendre kiábrándult népesség körében arra, hogy valaki betöltse; és konkrétan Bajnai személyét illetőleg is már jóval október 23-a előtt is már-már messianisztikus várakozás alakult ki, hogy vállakozik e tér betöltésére (vö. pl. szakmailag.tumblr.com/post/24531556503/haza-es-lebeges-bajnai-visszatert, kelt 12.06.06).
A konzervatív uraknak most valami újat mondtam? Piaci rés betöltése robbanásszerű felfutást eredményez.
A centrumból réges-rég kivonult mindenki, iszonyatos űr tátong ott, és nagyon erős keresleti igény van a 8 év ballib, majd 2 év fidesznyik kormányzásból rendre kiábrándult népesség körében arra, hogy valaki betöltse; és konkrétan Bajnai személyét illetőleg is már jóval október 23-a előtt is már-már messianisztikus várakozás alakult ki, hogy vállakozik e tér betöltésére (vö. pl. szakmailag.tumblr.com/post/24531556503/haza-es-lebeges-bajnai-visszatert, kelt 12.06.06).
A konzervatív uraknak most valami újat mondtam? Piaci rés betöltése robbanásszerű felfutást eredményez.
malvázia
2012.11.12 16:28:34
@tevevanegypupu: én nem értékítéletet mondtam pro v. kontra Bajnai, pusztán a szelek fújásáról meg a zászlók állásáról beszéltem afféle jó törökgáborosan.

Dehogyis Bajnai az ellenzéki szuperfegyver!Hanem például a szenátorasszony. Aki megszólalt. Újra.
Minden megszólalása aranyat ér: az ellenzék számára. És aki mindezért a fizetést adja neki, az nem veszi észre.
És szerencsére nem prototípus ez a fegyver. Vannak még.
Itt van…..

Szeretnék néha szirénát szerelni a fejemre. Valami nagy-nagy-tüzet kéne nyitni. Mert amit Schmitt Pál és a hozzá hasonló majomságok elfedenek, az valójában borzasztó. Az Új Elkúrás tanúi vagyunk. Mert mi az elkúrás? Mi volt Gyurcsány felejthetetlen bűne, amit 2004 és 2006…..

A Common Sense Society szeretettel meghívja a The Hungarian Political System könyv bemutatójával egybekötött Critical Elections 2010: Tectonic Changes in Hungarian Politics angol nyelvű, interaktív panelbeszélgetésre Tóth Csaba (szerző, Republikon), Héjj Dávid (Századvég) és…..
Belépve többet láthatsz. Itt beléphetsz
