Adatok
quodlibet
207 bejegyzést írt és 276 hozzászólása volt az általa látogatott blogokban.
Curt Jaimungal beszélgetése Bas van Fraassennel
Meglehetősen hosszú, de érdemes végig hallgatni (angolul van - de bekapcsolható hozzá fordítás). Nagyon sok témát érint, sajnos közben reklámok is vannak, de ki lehet bírni...
Filozófiai Széljegyzetek
Ahogy én látom a kortárs filozófia általam érzékelt szegmensét
2021.03.14 08:37:46
``A filozófia baglya a beálló alkonnyal kezdi meg röptét.'' mondja nekünk Hegel, és igaza van. Hogy mi a tudomány és mi a filozófia, az mindig a jelenből kiindulva, visszatekintve látszik. Azok a régi írások részei a tudomány történetének, amelyek a rokonsági és leszármazotti viszonyok alapján a mai…..
quodlibet
2025.12.16 18:41:19
Érdemes ezt meghallgatni: tilos.hu/episode/amirol-nem-lehet-beszelni/2025/12/08
Senki sem tudja, hogy meddig őrzi meg az internet a mindenkori jelen lenyomatait. Amikor a 90-es évek közepén elindult a honlapok világa, nagy lelkesen úgy gondoltam, hogy aki nincs fenn a neten, az nem is létezik. Ma már ebben korántsem vagyok biztos, de talán segít elodázni a felejtést egy régi…..
Megy a vita arról, hogy mit is akar a Tisza párt az adókkal és egyebekkel. És senki nem kezd el kiabálni, üvölteni, pedig azt kéne: hívjátok be őket a köztévébe és majd ők maguk elmondják, ez lenne a hiteles forrás. Lehet vitatkozni álkérdéseken, ennyire le vannak butítva a népek.
Majd áprilisban…..
quodlibet
2025.12.07 23:45:02
@nemecsekerno_007: Nagyon köszi, igazad van.
A fotó 1986 júliusában Mezőkövesden készült a kertben, a háttérben az új ház látszik, amelyik a 70-es években épült, és akkoriban még négy Borbála volt körülöttünk, dédnagymama, nagymama, feleségem és lányom. Hová lett a múlt, ami az igazságalkotója a fotónak?
..
Sündisznóállásban
Magyar Péter ünnepi beszéde 2025. október 23-án, a Hősök terén
2025.10.23 22:45:13
„Csoda, csoda, mert egységbe forrt megannyi különböző ember. A szabadság erei patakokba, a patakok folyókba, a szabadság mindent elsöprő erejű folyójába torkolltak. A Duna fölött aznap párába burkolózott a város. A fákon már csak néhány levél sápadtan kapaszkodott, de azon a napon Budapest és az…..
A teljesség igénye nélkül.
Év Csata / Ütközet Ellenfél Jelleg / Jelentőség
899 Brenta / Itáliai király Lambert Kalandozások fényes győzelme.
907 Pozsony / Bajorok A magyar államiság megszilárdulása.910 Rednitz / Frank–szász had A nyugati hatalmak visszaszorítása.
1285 Második tatárjárás /…..
Apám András Tibor, 1944. október 10-én, Kremenec/Kremenchuk mellett (apám mindig Kremjanec-nek mondta), szovjet-orosz fogságba esett. Ez egy ideiglenes fogolytábor volt, később tovább szállították a foglyokat. Volt a tábor mellett egy kisebb falu, ahol már egyáltalán nem voltak férfiak. Vagy…..
Szerintem a „Kétréses, késleltetett választás kvantum-törlés kísérlet” a modern fizika legfontosabb, zavarba ejtő kísérlete. Sokan ismertetik és magyarázzák ezeket a híres kísérleteket, de talán az alábbi az egyik legvilágosabb leírása a kísérleteknek. Ha jól figyelsz az alábbi videóra te is…..
Az alábbi táblázat olyan (nem teljes) névsor, akik Putyin rendszerének prominens kritikusai vagy kényes ügyeinek szereplői voltak, és erőszakos vagy erősen gyanús körülmények között haltak meg. Természetesen a gyilkosok tagadnak, maszatolnak, terelnek, és a támogatóik erre…..
A kérdés
A Quora levelezőlistán írja Viktor T. Toth fizikus-informatikus (én 2025. március 5-én kaptam meg az emailt, de az eredeti válasz dátumozása február 8.).[1]
Kérdés:[2] „Ha bebizonyosodik, hogy a téridő nem alapvető és lényegi *alkotórésze a fizikai valóságnak*, hanem inkább emergens és…..
Az 1985-ban írt szakdolgozatomnak ez volt a címe: „Törvényszerűségek és véges automaták” , jó hosszú volt, 172 oldal, bíráló tanár Faragó Szabó István. (Jó egészséget kívánok tanár úrnak!) Akkoriban az okság, determinizmus és szabadság kérdése foglalkoztatott, de észrevettem, hogy ezek az…..
quodlibet
2025.06.12 13:34:05
Hétvégén Martin Heidegger Bevezetés a metafizikába c. könyvét olvastam. Ez a kötet Heidegger 1935-ben tartott előadássorozatának szövegét tartalmazza, amelyet szerkesztve 1953-ban publikált. Heidegger olvasásához egy nemrég megjelent hír adta az ötletet és a kedvet, mely a…..
quodlibet
2025.06.01 18:04:40
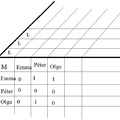
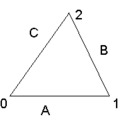
1. Indexek és relációk
Nekem úgy tűnik sok filozófus óvatos távolságtartással kezeli a relációkat, és sokan bizonyos előítéletekkel közelítenek ehhez a kategóriához. A következőekben azt szeretném elmondani, hogy én miért nem tartom szerencsésnek, ha indexekről beszélünk relációk helyett. Egyszerű…..
Akkor öregszünk meg, amikor már csak a régi nótát fújjuk, azt ismételgetjük, amit fiatal korunkban tanultunk, miközben annak a nagy része mára már elavult. Amikor már fejlődésképtelenek vagyunk, leálltunk, leszálló ágba kerültünk. Ez jutott eszembe, amikor olvastam az ÉS 2024/51-52 számában Bokros…..
Futólag átnézve a szövegeket, nem csak elütéseket, hanem ábrákkal kapcsolatos hibákat is találtam. Ezeket amint időm lesz, kijavítom. A szövegekből kiviláglik, hogy korábban az idő 'B' teóriáját fogadtam csak el, mint ami összhangban van a természettudományokkal. Erről egy ideje másképp…..
2024 szilvesztere az újévi beszédek sokaságát hozta. A teljesség igénye nélkül alább lehet választani.
Magyar Péter beszéde 11:53-tól indul:https://www.youtube.com/watch?v=najk3UR_YFc&t=655s
Karácsony Gergely:https://www.youtube.com/watch?v=wkyL458LWoY
Menczer…..
Andrés Gallois változással kapcsolatos gondolatiról írt 54. posztomat újra olvasva észrevettem, hogy bajok vannak az én formális logikai fordításommal. Gallois 2017-es, a változás lehetőségét taglaló álláspontját elemző részben lefordítom formális logikai nyelvre Gallois gondolatait. Rájöttem, hogy…..
Többször írtam erről a nevezetes filozófiai rejtvényről. André Gallois és Daniel Z. Korman is foglalkozott a problémával, írtam róluk. A 2018-as posztom tartalmazza Jennifer Wang előadásának leírt változatát, érdemes elolvasni, mert Wang lát megoldást. Azóta többször foglalkoztam a kérdéssel,…..
Bevezetés
Alább összefoglalom és kiegészítem azokat a gondolatokat, amiket korábbi írásaimban elszórtan a szabad akaratról mondtam.
A szabad akarat, mint filozófiai fogalom, mint filozófiai probléma szorosan kapcsolódik néhány másik kérdéshez, amelyeket szintén tárgyaltam más írásaimban, de most a…..
A Novaja Zemlja szigetcsoport az egyik legintenzívebben bombázott hely bolygónkon. Oroszország északi partjainál, a Jeges-tengeren, úgy lóg ki ez a földrész, mint egy fájó hüvelykujj. Ez egy olyan hely, amelyet biztosan észrevettél, ha valaha is ránéztél Oroszország térképére. És mégis, ez egy olyan…..
Házunkban lakott egy maszek kalapos, Virág kalaposnak hívták. Neki még autója is volt, ha jól emlékszem, egy Skoda. A harmadikon laktak. A harcok idején együtt voltunk velük a pincében. Virág bácsinak a József krt. 21. ház kapujától balra volt a boltja, ott volt a kirakata is. 1956-ban a forradalom…..
Az előző poszt folytatása
Egyedül vagyunk az univerzumban? Biztos választ csak arra kaphatunk, hogy nem vagyunk egyedül; akkor kapnánk biztos választ, ha találkoznánk idegen civilizációkkal vagy azok üzeneteivel. A negatív válasz tapasztalatilag igazolhatatlan, hisz lehetetlen a felfoghatatlan…..
Filozófiai Széljegyzetek
Világok sokasága, avagy a kozmológiai végtelen paradoxona
2024.10.10 11:21:18
1. Bevezetés
Gyakran nézegetek népszerű tudományos oldalakat, próbálok minél többet megérteni a modern fizikából. Különösen érdekes ezen belül a kozmológia, most főleg erről lesz szó.[1] Engem a világ időbeli és térbeli végessége vagy végtelensége érdekel elsősorban, és ezek a népszerű ismertetők…..
Mácsai Csernovics Emília (Arad, 1819. november 19. – Budapest, 1909. november 30.) Damjanich János honvéd vezérőrnagy és aradi vértanú felesége
*** Akik előttünk éltek ***
„A nemesi származású mácsai Csernovics család sarja. Férjéhez hasonlóan szerb származású volt. Emília Aradon nevelkedett,…..
Belépve többet láthatsz. Itt beléphetsz