Adatok
mitlaendre
8 bejegyzést írt és 2 hozzászólása volt az általa látogatott blogokban.

Létezik jól meghatározott eljárás arra hogy véletlenszerűen számot generáljunk? Hogyan veszik a számítógépek a véletlen számokat?..

Rengeteg ügyes módszer létezik a francia kártyapakli keverésére, de lehetséges hogy véletlenül ugyan úgy kevertük meg újra a paklit? Hányféleképpen is lehet megkeverni az 52 lapot?..

A közismert 6-oldalú dobókockával bizonyára mindenki "generált" már 1 és 6 közt véletlen számot. De milyen intervallumokra lehetséges még a generálás?..
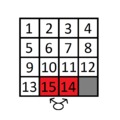
A 19. században Sam Loyd 1000$ nyereményt ajánlott fel annak, aki meg bírja oldani a 15-ös játékban a 14 és 15-ös elemek felcserélését. Ez már akkor is bizonyítottan lehetetlen volt, viszont egy apró változtatással megoldhatóvá válik...

Isten száma alatt általában a matematikusok azt a számot értik, ahány forgatással a hagyományos 3x3x3-as Rubik-kockát bármely állásából a kész állásba lehet forgatni. Na de mennyi is ez a szám?..

A matematikát bár a logika irányítja, mégis előfordul sokszor hogy logikátlannak tűnik egy bizonyosság.Az ilyen furcsaságokból gyűjtöttünk össze véletlenszerűen néhányat:..

A dobótestek olyan testek, amelyek azonos valószínűséggel esnek bármelyik oldalukra. Ilyen pl. a dobókocka.A legtöbb hétköznapi dobótest valamilyen szabályos test, de bármilyen más oldalszámra is létezik dobótest?..
mitlaendre
2021.11.17 20:09:51
@phls: A térszögekkel vett arány már a videóban is előkerült (gömbbe helyezték a hengert), de ott szignifikáns eltérést tapasztaltak a gyakorlatban kapott dobások száma, és az elméletben várt dobások száma közt.
Síklapokkal határolt testek esetén is ehhez hasonló becsléseket lehet tenni, de a tényleges magasság megtalálásának bizonyítására itt is statisztikai eszközöket kell alkalmaznunk, hiszen pontosan egy elmélet azon tulajdonságát szeretnénk vizsgálni, hogy mennyire jól modellezi a valós eseményeket.
Arra, hogy mi lehet a térszögnél jobb becslés, csak ötletek vannak.
Legjobban célravezető talán az lenne, ha egy N oldalú szabályos sokszög alapú hasábnál néznénk az oldalmetszetet.
(Mivel a hasáb magassággal párhuzamos, súlyponton áthaladó tengelyére való forgatás számunkra irreleváns. Hiszen két oldallap közötti esetleges átfordulás nem változtathat az eloszláson, hiszen azok mindenképpen egyenlő valószínűséggel rendelkeznek.)
Ekkor csak azt kell kiszámolnunk, hogy egy tetszőlegesen kiválasztott oldallapról milyen "valószínűséggel" vagyis mekkora energia kell ahhoz hogy egy oldallap felé, és mekkora energia kell ahhoz hogy az egyik N-szöglap felé forduljon át az adott test.
Ha ennek a két forduláshoz szükséges energiának az arányát jól ki tudjuk választani, akkor elviekben meg tudjuk határozni a kellő magasságot.
Az, hogy ez az elmélet mennyire működik a gyakorlatban, kísérletezés és statisztikai vizsgálat szükséges még.
Síklapokkal határolt testek esetén is ehhez hasonló becsléseket lehet tenni, de a tényleges magasság megtalálásának bizonyítására itt is statisztikai eszközöket kell alkalmaznunk, hiszen pontosan egy elmélet azon tulajdonságát szeretnénk vizsgálni, hogy mennyire jól modellezi a valós eseményeket.
Arra, hogy mi lehet a térszögnél jobb becslés, csak ötletek vannak.
Legjobban célravezető talán az lenne, ha egy N oldalú szabályos sokszög alapú hasábnál néznénk az oldalmetszetet.
(Mivel a hasáb magassággal párhuzamos, súlyponton áthaladó tengelyére való forgatás számunkra irreleváns. Hiszen két oldallap közötti esetleges átfordulás nem változtathat az eloszláson, hiszen azok mindenképpen egyenlő valószínűséggel rendelkeznek.)
Ekkor csak azt kell kiszámolnunk, hogy egy tetszőlegesen kiválasztott oldallapról milyen "valószínűséggel" vagyis mekkora energia kell ahhoz hogy egy oldallap felé, és mekkora energia kell ahhoz hogy az egyik N-szöglap felé forduljon át az adott test.
Ha ennek a két forduláshoz szükséges energiának az arányát jól ki tudjuk választani, akkor elviekben meg tudjuk határozni a kellő magasságot.
Az, hogy ez az elmélet mennyire működik a gyakorlatban, kísérletezés és statisztikai vizsgálat szükséges még.
A zenében gyakran felfedezhetőek matematikai motívumok, viszont Bach kánonjai ilyen szempontból kiemelkedőnek számítanak...
Belépve többet láthatsz. Itt beléphetsz

Az elejétől vett első "centi" felület ekkor alulról becsülhető egy kellően kicsi 0< Epszilon * "1 centi" téglalappal, amin a festék mennyisége mindenképpen elszáll a végtelenbe, hiszen 1/x integrálja a (0,1) intervallumon végtelen. Ekkor a kis téglalapon lévő festék mennyisége is Epszilon * végtelen lenne.
Így bár a harsona végtelen hosszú nyúlványához elég lenne véges mennyiségű festék, de az első "1 centi"-hez nem. Viszont a harsona elejétől 1/(x+1) rétegvastagsággal már szerintem megoldható.
Ekkor a számításaim szerint ~6,782255 egységnyi festékkel le lehet festeni a harsonát, már ha az "1 centi" a harsona konstrukciójában szereplő egységgel egyezik meg.