Adatok
measure41
0 bejegyzést írt és 36 hozzászólása volt az általa látogatott blogokban.
Összefoglalás: Megmutatom, hogy a természetes számok halmaza, hibás definícióinak (axiómáinak) köszönhetően, nem megszámlálható, azaz kontinuum számosságú, szemben a korábbi feltételezéssel, és szándékkal, mely szerint a természetes számok halmaza megszámlálhatóan végtelen számosságú. A természetes…..
measure41
2016.11.15 13:49:21
Harmadrészt, pedig ahhoz képest, hogy már megismerte "természetes számok valóságos természetét", a felmerülő problémákat igen gyakran csak ellentmondásosan tudta "megoldani", például, ön rendszeresen végtelen természetes számOKról beszél, majd kijelenti: ∞ = ∞+1 (melyről megmutattam, hogy a halmazelméleti modellel egyértelműen ellentmondásos), ezzel az Ön által határértékként felfogott végtelen természetes számból rákövetkezéssel csak saját magát tudja implikálni, így az innentől vett sorozat konstans, tehát "határértékképzéssel" sem tud újabb végtelen számokat "generálni", ami pedig ellentmondásban van a többesszámmal, és a megszámlálhatatlansággal.
X halmaz azon elemekből áll, amelyek nem elemei X-nek.
A Russell paradoxon:
Tekintsük az összes önmagukat nem tartalmazó halmazok G gyűjtőhalmazát. Vajon ez a G gyűjtőhalmaz tartalmazza-e önmagát? A kérdés eldönthetetlen. Ugyanis ha nem tartalmazza, akkor ez egy olyan halmaz, amelyik nem…..
measure41
2016.11.08 12:43:31
@Takács Ferenc bp.:
A Cantor tétel a természetes számok halmazára pontosan azt mondja ki, amit állít, hogy nem létezik olyan szürjektív megfeleltetés a természetes számok és annak hatványhalmaza között, tehát definíció szerint a természetes számok hatványhalmaza nagyobb számosságú mint a természetes számoké.
Olvastam a többi cikkét is, a H leképezésről, amivel, mint már többen rámutattak, az a probléma, hogy csak a véges részhalmazokra vonatkozik, tehát nem bijektív. Ezen problémát az Ön önkényes határérték felfogása sem oldja meg. Olyan konkrét természetes számot nem tud mondani, amire H értéke éppen a páros számok halmaza lenne, csupán megadott a természetes számoknak egy olyan részhalmazát, melynek elemein végiglépkedve a H értékének a "határértéke" éppen a páros számok halmaza, tehát lényegében kiterjesztette a H függvényt úgy, hogy a természetes számok adott részhalmazán is értelmezve legyen, tehát a természetes számok számosságát tekintve már irreleváns.
A Cantor tétel a természetes számok halmazára pontosan azt mondja ki, amit állít, hogy nem létezik olyan szürjektív megfeleltetés a természetes számok és annak hatványhalmaza között, tehát definíció szerint a természetes számok hatványhalmaza nagyobb számosságú mint a természetes számoké.
Olvastam a többi cikkét is, a H leképezésről, amivel, mint már többen rámutattak, az a probléma, hogy csak a véges részhalmazokra vonatkozik, tehát nem bijektív. Ezen problémát az Ön önkényes határérték felfogása sem oldja meg. Olyan konkrét természetes számot nem tud mondani, amire H értéke éppen a páros számok halmaza lenne, csupán megadott a természetes számoknak egy olyan részhalmazát, melynek elemein végiglépkedve a H értékének a "határértéke" éppen a páros számok halmaza, tehát lényegében kiterjesztette a H függvényt úgy, hogy a természetes számok adott részhalmazán is értelmezve legyen, tehát a természetes számok számosságát tekintve már irreleváns.

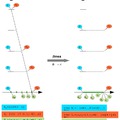
Itt egyszerű ponthalmazok leképezése látható. Az egyik ponthalmaz a természetes számok kezdőszelet halmazai (N), a másik halmaz (V) a függőleges tengelynek támaszkodó egyenes egész koordinátákat metsző pontjai, a harmadik ponthalmaz (P) ezek vetülete a vízszintes tengelyen. Az…..
Belépve többet láthatsz. Itt beléphetsz
